9536. Sum of matrices

Given two matrices A and B. Find their sum C = A + B.

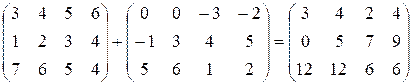
Input. The first line contains the dimensions of the matrices – two integers n and m (1 ≤ n, m ≤ 100).

Then follow n lines with m integers each, describing matrix A. After that comes an empty line, followed by matrix B given in the same format.

Output. Print matrix С: n lines with m integers.

Sample input	Sample output
3 4 3 4 5 6 1 2 3 4 7 6 5 4 0 0 -3 -2 -1 3 4 5 5 6 1 2	3 4 2 4 0 5 7 9 12 12 6 6

SOLUTION

algebra

Algorithm analysis

Given matrices А and В, compute their sum – the matrix С, where

С_ij = A_ij + B_ij

Algorithm implementation

Declare the matrices a, b and c.

#define MAX 101

int a[MAX][MAX], b[MAX][MAX], c[MAX][MAX];

Read the input data – matrices А and В.

scanf("%d %d", &n, &m);

for (i = 0; i < n; i++)

for (j = 0; j < m; j++)

scanf("%d", &a[i][j]);

for (i = 0; i < n; i++)

for (j = 0; j < m; j++)

scanf("%d", &b[i][j]);

Compute the sum of the matrices: C = A + B.

for (i = 0; i < n; i++)

for (j = 0; j < m; j++)

c[i][j] = a[i][j] + b[i][j];

Print the resulting matrix.

for (i = 0; i < n; i++)

{

for (j = 0; j < m; j++)

printf("%d ", c[i][j]);

printf("\n");

}

Algorithm implementation – double pointer

Declare the matrices a, b and c as double pointers.

int **a, **b, **c;

The function Read reads the matrix matr.

void Read(int **&matr, int n, int m)

{

matr = new int* [n];

for (i = 0; i < n; i++)

{

matr[i] = new int[m];

for (j = 0; j < m; j++)

scanf("%d", &matr[i][j]);

}

}

The function Sum computes the sum of the matrices A + B and stores it in matrix C.

void Sum(int **a, int **b, int **&c, int n, int m)

{

c = new int* [n];

for (i = 0; i < n; i++)

{

c[i] = new int[m];

for (j = 0; j < m; j++)

c[i][j] = a[i][j] + b[i][j];

}

}

The function Print prints matrix A.

void Print(int **a)

{

for (i = 0; i < n; i++)

{

for (j = 0; j < m; j++)

printf("%d ", a[i][j]);

printf("\n");

}

}

The main part of the program. Read the dimensions of the matrices n and m.

scanf("%d %d", &n, &m);

Read the matrices a and b.

Read(a, n, m);

Read(b, n, m);

Compute the sum of the matrices C = A + B.

Sum(a, b, c, n, m);

Print the resulting matrix.

Print(c);